Barisan Berderajat

1. Barisan berderajat satu
Barisan berderajat satu yaitu barisan yang mempunyai selisih tetap pada tingkat pertama penyelidikan


Contoh: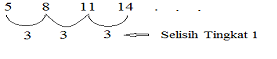 
Bentuk umum barisan tersebut adalah
Un = an + b
U1 = a + b
U2= 2a + b
Dan seterusnya
Sehingga di peroleh:





Untuk barisan 5, 8, 11, 14, … diperoleh a = 3. Nilai b diperoleh dengan mensubstitusi ke U1 sehingga diperoleh



Bagaimana untuk berderajat dua dan seterusnya?




2. Barisan berderajat dua
Barisan berderajat dua yaitu barisan yang memiliki selisih tetap pada tinggkat ke dua penyelidikan
Contoh



Bentuk umum barisan tersebut adalah
Un = an2 + bn + c
U1 = a(1)2 + b(1)+c = a + b + c
U2 = a(2)2 + b(2)+c = 4a + 2b + c
U3 = a(3)2 + b(3)+c = 9a +3 b + c
U4 = a(4)2 + b(4)+c = 16a +4 b + c
Dan seterusnya
Sehingga diperoleh



Untuk rumus suku ke-n dari barisan 5, 8, 13, 20, 29,…
Diperoleh:



3. Barisan berderajat Tiga
Barisan berderajat dua yaitu barisan yang memiliki selisih tetap pada tinggkat ke dua penyelidikan
Contoh



Bentuk umum barisan tersebut adalah
Un = an3 + bn2 + cn + d
U1 = a(1)3 + b(1)2 + c(1) + d = a + b + c + d
U2 = a(2)3 + b(2)2 + c(2) + d = 8a + 4b + 2c + d
U3 = a(3)3 + b(3)2 + c(3) + d = 27a + 9b + 3c + d
U4 = a(4)3 + b(4)2 + c(4) + d = 64a + 16b + 4c + d
Dan seterusnya
Sehingga diperoleh..



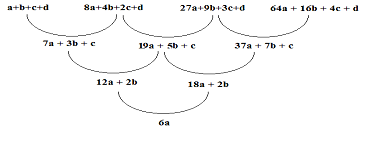
Untuk barisan di atas diperoleh




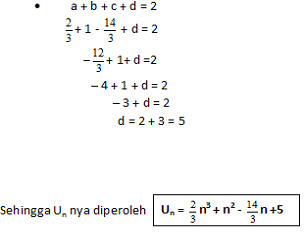
Itulah barisan berderajat 1, 2, dan 3. Untuk yang berderajat lebih dari 3 ilustrasinya sama dengan yang kita bahas tadi.